| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
|
Coombs' method is a ranked voting system. Like instant-runoff (IRV-RCV), Coombs' method is a sequential-loser method, where the last-place finisher according to one method is eliminated in each round. However, unlike in instant-runoff, each round has electors voting against their least-favorite candidate; the candidate ranked last by the most voters is eliminated.[1]
The method fails most voting system criteria, including Condorcet's majority criterion, monotonicity, participation, and clone-independence.[2][3] However, it does satisfy the median voter criterion.
History
[edit]The method was popularized by Clyde Coombs.[1] It was described by Edward J. Nanson as the "Venetian method",[4] but should not be confused with the Republic of Venice's use of score voting in elections for Doge.
Procedures
[edit]Each voter rank-orders all of the candidates on their ballot. Otherwise, the candidate ranked last by the largest number (plurality) of voters is eliminated, making each individual round equivalent to anti-plurality voting. Conversely, under instant-runoff voting, the candidate ranked first (among non-eliminated candidates) by the fewest voters is eliminated.
In some sources, the elimination proceeds regardless of whether any candidate is ranked first by a majority of voters, and the last candidate to be eliminated is the winner.[5] This variant of the method can result in a different winner than the former one (unlike in instant-runoff voting, where checking to see if any candidate is ranked first by a majority of voters is only a shortcut that does not affect the outcome).
An example
[edit]
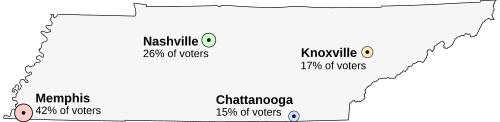
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
Assuming all of the voters vote sincerely (strategic voting is discussed below), the results would be as follows, by percentage:
| City | Round 1 | Round 2 | ||
|---|---|---|---|---|
| First | Last | First | Last | |
| Memphis | 42 | 58 | ||
| Nashville | 26 | 0 | ||
| Chattanooga | 15 | 0 | 15 | |
| Knoxville | 17 | 42 | 17 | |
- In the first round, no candidate has an absolute majority of first-place votes (51).
- Memphis, having the most last-place votes (26+15+17=58), is therefore eliminated.
- In the second round, Memphis is out of the running, and so must be factored out. Memphis was ranked first on Group A's ballots, so the second choice of Group A, Nashville, gets an additional 42 first-place votes, giving it an absolute majority of first-place votes (68 versus 15+17=32), and making it the winner.
- Note that the last-place votes are only used to eliminate a candidate in a voting round where no candidate achieves an absolute majority; they are disregarded in a round where any candidate has more than 50%. Thus last-place votes play no role in the final round.
In practice
[edit]The voting rounds used in the reality television program Survivor could be considered a variation of Coombs' method but with sequential voting rounds. Everyone votes for one candidate they support for elimination each round, and the candidate with a plurality of that vote is eliminated. A strategy difference is that sequential rounds of voting means the elimination choice is fixed in a ranked ballot Coombs' method until that candidate is eliminated.
Potential for strategic voting
[edit]Like anti-plurality voting, Coombs' rule is extremely vulnerable to strategic voting. As a result, it is more often considered as an example of a pathological voting rule than it is a serious rule.[6] Coombs' method is extremely sensitive to incomplete ballots, compromising, push-over, and teaming, and the vast majority of voters' effects on the election come from how they fill out the bottom of their ballots.[6] As a result, voters have a strong incentive to rate the strongest candidates last to defeat them in earlier rounds.[7]
This results in a Keynesian beauty pageant that is extremely sensitive to minor variations in the perceived strengths of candidates.
See also
[edit]Notes
[edit]- ^ a b Grofman, Bernard, and Scott L. Feld (2004) "If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule," Electoral Studies 23:641-59.
- ^ Nurmi, Hannu (1983-04-01). "Voting Procedures: A Summary Analysis". British Journal of Political Science. 13 (2). Cambridge University Press: 181–208. doi:10.1017/S0007123400003215. Retrieved 2024-05-19.
- ^ Nurmi, Hannu (2012-12-06). Comparing Voting systems. Theory and Decision Library A. Vol. 3 (Illustrated ed.). Springer Dordrecht. p. 209. doi:10.1007/978-94-009-3985-1. ISBN 9789400939851.
- ^ Royal Society of Victoria (Melbourne, Vic ) (1864). Transactions and proceedings of the Royal Society of Victoria . American Museum of Natural History Library. Melbourne : The Society.
- ^ Pacuit, Eric, "Voting Methods", The Stanford Encyclopedia of Philosophy (Fall 2017 Edition), Edward N. Zalta (ed.)
- ^ a b "Data on Manipulability"
- ^ Smith, Warren D. (12 July 2006). "Descriptions of single-winner voting systems" (PDF). Voting Systems.