In mathematics, a power series (in one variable) is an infinite series of the form where an represents the coefficient of the nth term and c is a constant called the center of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function.
In many situations, the center c is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form
The partial sums of a power series are polynomials, the partial sums of the Taylor series of an analytic function are a sequence of converging polynomial approximations to the function at the center, and a converging power series can be seen as a kind of generalized polynomial with infinitely many terms. Conversely, every polynomial is a power series with only finitely many non-zero terms.
Beyond their role in mathematical analysis, power series also occur in combinatorics as generating functions (a kind of formal power series) and in electronic engineering (under the name of the Z-transform). The familiar decimal notation for real numbers can also be viewed as an example of a power series, with integer coefficients, but with the argument x fixed at 1⁄10. In number theory, the concept of p-adic numbers is also closely related to that of a power series.
Examples
Polynomial
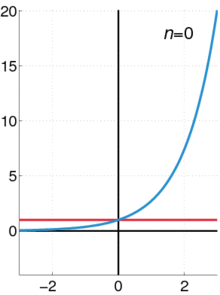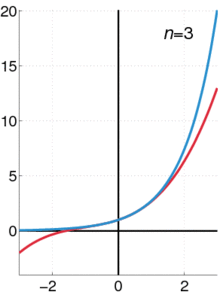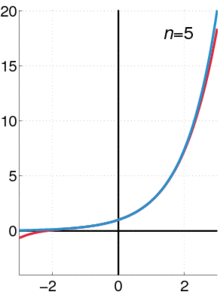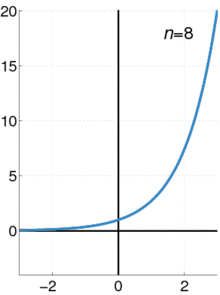
n=0 gives ,
n=1 ,
n=2 ,
n=3 etcetera.
Every polynomial of degree d can be expressed as a power series around any center c, where all terms of degree higher than d have a coefficient of zero.[1] For instance, the polynomial can be written as a power series around the center as or around the center as
One can view power series as being like "polynomials of infinite degree", although power series are not polynomials in the strict sense.
Geometric series, exponential function and sine
The geometric series formula which is valid for , is one of the most important examples of a power series, as are the exponential function formula and the sine formula valid for all real x. These power series are examples of Taylor series (or, more specifically, of Maclaurin series).
On the set of exponents
Negative powers are not permitted in an ordinary power series; for instance, is not considered a power series (although it is a Laurent series). Similarly, fractional powers such as are not permitted; fractional powers arise in Puiseux series. The coefficients must not depend on , thus for instance is not a power series.
Radius of convergence
A power series is convergent for some values of the variable x, which will always include x = c since and the sum of the series is thus for x = c. The series may diverge for other values of x, possibly all of them. If c is not the only point of convergence, then there is always a number r with 0 < r ≤ ∞ such that the series converges whenever |x – c| < r and diverges whenever |x – c| > r. The number r is called the radius of convergence of the power series; in general it is given as or, equivalently, This is the Cauchy–Hadamard theorem; see limit superior and limit inferior for an explanation of the notation. The relation is also satisfied, if this limit exists.
The set of the complex numbers such that |x – c| < r is called the disc of convergence of the series. The series converges absolutely inside its disc of convergence and it converges uniformly on every compact subset of the disc of convergence.
For |x – c| = r, there is no general statement on the convergence of the series. However, Abel's theorem states that if the series is convergent for some value z such that |z – c| = r, then the sum of the series for x = z is the limit of the sum of the series for x = c + t (z – c) where t is a real variable less than 1 that tends to 1.
Operations on power series
Addition and subtraction
When two functions f and g are decomposed into power series around the same center c, the power series of the sum or difference of the functions can be obtained by termwise addition and subtraction. That is, if and then
The sum of two power series will have a radius of convergence of at least the smaller of the two radii of convergence of the two series,[2] but possibly larger than either of the two. For instance it is not true that if two power series and have the same radius of convergence, then also has this radius of convergence: if and , for instance, then both series have the same radius of convergence of 1, but the series has a radius of convergence of 3.
Multiplication and division
With the same definitions for and , the power series of the product and quotient of the functions can be obtained as follows:
The sequence is known as the Cauchy product of the sequences and .
For division, if one defines the sequence by then and one can solve recursively for the terms by comparing coefficients.
Solving the corresponding equations yields the formulae based on determinants of certain matrices of the coefficients of and
Differentiation and integration
Once a function is given as a power series as above, it is differentiable on the interior of the domain of convergence. It can be differentiated and integrated by treating every term separately since both differentiation and integration are linear transformations of functions:
Both of these series have the same radius of convergence as the original series.
Analytic functions
A function f defined on some open subset U of R or C is called analytic if it is locally given by a convergent power series. This means that every a ∈ U has an open neighborhood V ⊆ U, such that there exists a power series with center a that converges to f(x) for every x ∈ V.
Every power series with a positive radius of convergence is analytic on the interior of its region of convergence. All holomorphic functions are complex-analytic. Sums and products of analytic functions are analytic, as are quotients as long as the denominator is non-zero.
If a function is analytic, then it is infinitely differentiable, but in the real case the converse is not generally true. For an analytic function, the coefficients an can be computed as
where denotes the nth derivative of f at c, and . This means that every analytic function is locally represented by its Taylor series.
The global form of an analytic function is completely determined by its local behavior in the following sense: if f and g are two analytic functions defined on the same connected open set U, and if there exists an element c ∈ U such that f(n)(c) = g(n)(c) for all n ≥ 0, then f(x) = g(x) for all x ∈ U.
If a power series with radius of convergence r is given, one can consider analytic continuations of the series, that is, analytic functions f which are defined on larger sets than { x | |x − c| < r } and agree with the given power series on this set. The number r is maximal in the following sense: there always exists a complex number x with |x − c| = r such that no analytic continuation of the series can be defined at x.
The power series expansion of the inverse function of an analytic function can be determined using the Lagrange inversion theorem.
Behavior near the boundary
The sum of a power series with a positive radius of convergence is an analytic function at every point in the interior of the disc of convergence. However, different behavior can occur at points on the boundary of that disc. For example:
- Divergence while the sum extends to an analytic function: has radius of convergence equal to and diverges at every point of . Nevertheless, the sum in is , which is analytic at every point of the plane except for .
- Convergent at some points divergent at others: has radius of convergence . It converges for , while it diverges for .
- Absolute convergence at every point of the boundary: has radius of convergence , while it converges absolutely, and uniformly, at every point of due to Weierstrass M-test applied with the hyper-harmonic convergent series .
- Convergent on the closure of the disc of convergence but not continuous sum: Sierpiński gave an example[3] of a power series with radius of convergence , convergent at all points with , but the sum is an unbounded function and, in particular, discontinuous. A sufficient condition for one-sided continuity at a boundary point is given by Abel's theorem.
Formal power series
In abstract algebra, one attempts to capture the essence of power series without being restricted to the fields of real and complex numbers, and without the need to talk about convergence. This leads to the concept of formal power series, a concept of great utility in algebraic combinatorics.
Power series in several variables
An extension of the theory is necessary for the purposes of multivariable calculus. A power series is here defined to be an infinite series of the form where j = (j1, …, jn) is a vector of natural numbers, the coefficients a(j1, …, jn) are usually real or complex numbers, and the center c = (c1, …, cn) and argument x = (x1, …, xn) are usually real or complex vectors. The symbol is the product symbol, denoting multiplication. In the more convenient multi-index notation this can be written where is the set of natural numbers, and so is the set of ordered n-tuples of natural numbers.
The theory of such series is trickier than for single-variable series, with more complicated regions of convergence. For instance, the power series is absolutely convergent in the set between two hyperbolas. (This is an example of a log-convex set, in the sense that the set of points , where lies in the above region, is a convex set. More generally, one can show that when c=0, the interior of the region of absolute convergence is always a log-convex set in this sense.) On the other hand, in the interior of this region of convergence one may differentiate and integrate under the series sign, just as one may with ordinary power series.[4]
Order of a power series
Let α be a multi-index for a power series f(x1, x2, …, xn). The order of the power series f is defined to be the least value such that there is aα ≠ 0 with , or if f ≡ 0. In particular, for a power series f(x) in a single variable x, the order of f is the smallest power of x with a nonzero coefficient. This definition readily extends to Laurent series.
Notes
- ^ Howard Levi (1967). Polynomials, Power Series, and Calculus. Van Nostrand. p. 24.
- ^ Erwin Kreyszig, Advanced Engineering Mathematics, 8th ed, page 747
- ^ Wacław Sierpiński (1916). "Sur une série potentielle qui, étant convergente en tout point de son cercle de convergence, représente sur ce cercle une fonction discontinue. (French)". Rendiconti del Circolo Matematico di Palermo. 41. Palermo Rend.: 187–190. doi:10.1007/BF03018294. JFM 46.1466.03. S2CID 121218640.
- ^ Beckenbach, E. F. (1948). "Convex functions". Bulletin of the American Mathematical Society. 54 (5): 439–460. doi:10.1090/S0002-9904-1948-08994-7.
References
- Solomentsev, E.D. (2001) [1994], "Power series", Encyclopedia of Mathematics, EMS Press