| ||||
|---|---|---|---|---|
| Cardinal | fifty-four | |||
| Ordinal | 54th (fifty-fourth) | |||
| Factorization | 2 × 33 | |||
| Divisors | 1, 2, 3, 6, 9, 18, 27, 54 | |||
| Greek numeral | ΝΔ´ | |||
| Roman numeral | LIV, liv | |||
| Binary | 1101102 | |||
| Ternary | 20003 | |||
| Senary | 1306 | |||
| Octal | 668 | |||
| Duodecimal | 4612 | |||
| Hexadecimal | 3616 | |||
| Eastern Arabic, Kurdish, Persian, Sindhi | ٥٤ | |||
| Assamese & Bengali | ৫৪ | |||
| Chinese numeral, Japanese numeral | 五十四 | |||
| Devanāgarī | ५४ | |||
| Ge'ez | ፶፬ | |||
| Georgian | ნდ | |||
| Hebrew | נ"ד | |||
| Kannada | ೫೪ | |||
| Khmer | ៥៤ | |||
| Armenian | ԾԴ | |||
| Malayalam | ൫൰൪ | |||
| Meitei | ꯵꯴ | |||
| Thai | ๕๔ | |||
| Telugu | ౫౪ | |||
| Babylonian numeral | 𒐐𒐘 | |||
| Egyptian hieroglyph | 𓎊𓏽 | |||
| Mayan numeral | 𝋢𝋮 | |||
| Urdu numerals | ۵۴ | |||
| Tibetan numerals | ༥༤ | |||
| Financial kanji/hanja | 五拾四, 伍拾肆 | |||
| Morse code | ........._ | |||
| NATO phonetic alphabet | FIFE FOW-ER | |||
| ASCII value | 6 | |||
54 (fifty-four) is the natural number and positive integer following 53 and preceding 55. As a multiple of 2 but not of 4, 54 is an oddly even number and a composite number.
In mathematics
Number theory
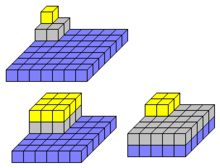
54 is an abundant number[1] because the sum of its proper divisors (66),[2] which excludes 54 as a divisor, is greater than itself. Like all multiples of 6,[3] 54 is equal to some of its proper divisors summed together,[a] so it is also a semiperfect number.[4] These proper divisors can be summed in various ways to express all positive integers smaller than 54, so 54 is a practical number as well.[5] Additionally, as an integer for which the arithmetic mean of all its positive divisors (including itself) is also an integer, 54 is an arithmetic number.[6]
54 can be constructed mathematically in a variety of ways. It is the smallest number that can be expressed as the sum of three positive squares in more than two different ways.[b][7] It can also be expressed as twice the third power of 3, so it is a Leyland number.[c][8] Additionally, fifty-four objects can be positioned to construct the vertices of a polygon with nineteen sides, so 54 is an enneadecagonal number and the first 19-gonal number after 19 itself.[d][9]
Trigonometry and the golden ratio
If the complementary angle of a triangle's corner is 54 degrees, the sine of that angle is half the golden ratio.[10][11] This is because the corresponding interior angle is equal to π/5 radians (or 36 degrees).[e] If that triangle is isoceles, the relationship with the golden ratio makes it a golden triangle. The golden triangle is most readily found as the spikes on a regular pentagram.
If, instead, 54 is the length of a triangle's side and all the sides lengths are rational numbers, the 54 side cannot be the hypotenuse. Using the Pythagorean theorem, there is no way to construct 542 as the sum of two other square rational numbers. Therefore, 54 is a nonhypotenuse number.[12]
However, 54 can be expressed as the area of a triangle with three rational side lengths.[f] Therefore, it is a congruent number.[13] One of these combinations of three rational side lengths is composed of integers: 9:12:15, which is a 3:4:5 right triangle that is a Pythagorean, a Heronian, and a Brahmagupta triangle.
Regular number used in Babylonian mathematics
As a regular number, 54 is a divisor of many powers of 60,[g] which is an important property in Assyro-Babylonian mathematics because it uses a sexagesimal (base 60) number system. In base 60, the reciprocal of a regular number has a finite representation, and that simplified multiplication and division.[14] Babylonian calculators kept tables of these reciprocals in order to make their work more efficient.[15] For instance, 603 ÷ 54 = 4000. In base 60, division by 54 can be accomplished by multiplying by 4000 and shifting three places. In base 60, 4000 can be written as 1:6:40.[h] Thus, 1/54 can be written as 1×60-1 + 6×60-2 + 40×60-3, also denoted 1:6:40 as Babylonian notational conventions did not specify the power of the starting digit. Conversely 1/4000 = 54/603, so division by 1:6:40 = 4000 can be accomplished by instead multiplying by 54 and shifting three base-60 places.
List of basic calculations
| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 54 × x | 54 | 108 | 162 | 216 | 270 | 324 | 378 | 432 | 486 | 540 | 594 | 648 | 702 | 756 | 810 | 918 | 972 | 1026 | 1080 | 1134 |
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 54 ÷ x | 54 | 27 | 18 | 13.5 | 10.8 | 9 | 7.714285 | 6.75 | 6 | 5.4 | 4.90 | 4.5 | 4.153846 | 3.857142 | 3.6 |
| x ÷ 54 | 0.01851 | 0.037 | 0.05 | 0.074 | 0.0925 | 0.1 | 0.1296 | 0.148 | 0.16 | 0.185 | 0.2037 | 0.2 | 0.2407 | 0.259 | 0.27 |
| Exponentiation | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 54x | 54 | 2916 | 157464 | 8503056 | 459165024 |
| x54 | 1 | 18014398509481984 | 58149737003040059690390169 | 324518553658426726783156020576256 | 55511151231257827021181583404541015625 |
| 54 | 7.34846...[i] | 3.77976... | 2.71080... | 2.22064... |
In literature
In The Hitchhiker's Guide to the Galaxy by Douglas Adams, the "Answer to the Ultimate Question of Life, the Universe, and Everything" famously was 42.[17] Eventually, one character's unsuccessful attempt to divine the Ultimate Question elicited "What do you get if you multiply six by nine?"[18] The mathematical answer was 54, not 42. Some readers who were trying to find a deeper meaning in the passage soon noticed the fact was true in base 13: the base-10 expression 5410 can be encoded as the base-13 expression 4213.[19] Adams said this was a coincidence.[20]
Explanatory footnotes

- ^ 54 can be expressed as: 9 + 18 + 27 = 54.
- ^ 54 can be expressed as:
- 72 + 22 + 12 = 54
- 62 + 32 + 32 = 54
- 52 + 52 + 22 = 54
- ^ 54 can be expressed as: 33 + 33 = 54. A Leyland number is a number that can be expressed as xy + yx, so 54 is the Leyland number when x = y = 3.
- ^ To show this, make an inner shell of nineteen points at the regular polygon's vertices. By convention, choose one point of the inner shell that will be shared with an outer shell. Then, make that outer shell by placing thirty-five points (plus the one shared point) in segments two-points-long to represent the nineteen sides of a second regular polygon. 19 + 35 = 54.
- ^ There are various ways to prove this, but the algebraic method will eventually show that cos(π/5) = 2*sqrt(5)/4 = phi/2.
- ^ AreaΔ = 1/2 base × height. Therefore, a triangle with a base of 9 and a height of 12 has an area of 54. By the Pythagoean theorem, the hypotenuse of that triangle is 15.
- ^ 603 and its multiples are divisible by 54.
- ^ 1:6:40 = 1×602 + 6×601 + 40×600 = 4000. Although, these would have been written in actual Babylonian numerals.
- ^ Because 54 is a multiple of 2 but not a square number, its square root is irrational.[16]
References
- ^ Sloane, N. J. A. (ed.). "Sequence A005101 (Abundant numbers (sum of divisors of m exceeds 2m))". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A001065 (Sum of proper divisors (or aliquot parts) of n: sum of divisors of n that are less than n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Zachariou, Andreas; Zachariou, Eleni (1972). "Perfect, Semiperfect and Ore Numbers". Bull. Soc. Math. Grèce. Nouvelle Série. 13: 12–22. MR 0360455. Zbl 0266.10012.
- ^ Sloane, N. J. A. (ed.). "Sequence A005835 (Pseudoperfect (or semiperfect) numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A005153 (Practical numbers: positive integers m such that every k <= sigma(m) is a sum of distinct divisors of m. Also called panarithmic numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A003601 (Numbers j such that the average of the divisors of j is an integer: sigma_0(j) divides sigma_1(j). Alternatively, numbers j such that tau(j) (A000005(j)) divides sigma(j) (A000203(j)).)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.), "Sequence A025331 (Numbers that are the sum of 3 nonzero squares in 3 or more ways.)", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation; Sloane, N. J. A. (ed.). "Sequence A025323 (Numbers that are the sum of 3 nonzero squares in exactly 3 ways.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A076980 (Leyland numbers: 3, together with numbers expressible as n^k + k^n nontrivially, i.e., n,k > 1 (to avoid n = (n-1)^1 + 1^(n-1)).)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A051871 (19-gonal (or enneadecagonal) numbers: n(17n-15)/2.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Khan, Sameen Ahmed (2020-10-11). "Trigonometric Ratios Using Geometric Methods". Advances in Mathematics: Scientific Journal. 9 (10): 8698. doi:10.37418/amsj.9.10.94. ISSN 1857-8365.
- ^ Sloane, N. J. A. (ed.). "Sequence A019863 (Decimal expansion of sin(3*Pi/10) (sine of 54 degrees, or cosine of 36 degrees).)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A004144 (Nonhypotenuse numbers (indices of positive squares that are not the sums of 2 distinct nonzero squares).)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A003273 (Congruent numbers: positive integers k for which there exists a right triangle having area k and rational sides.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Aaboe, Asger (1965), "Some Seleucid mathematical tables (extended reciprocals and squares of regular numbers)", Journal of Cuneiform Studies, 19 (3), The American Schools of Oriental Research: 79–86, doi:10.2307/1359089, JSTOR 1359089, MR 0191779, S2CID 164195082.
- ^ Sachs, A. J. (1947), "Babylonian mathematical texts. I. Reciprocals of regular sexagesimal numbers", Journal of Cuneiform Studies, 1 (3), The American Schools of Oriental Research: 219–240, doi:10.2307/1359434, JSTOR 1359434, MR 0022180, S2CID 163783242
- ^ Jackson, Terence (2011-07-01). "95.42 Irrational square roots of natural numbers — a geometrical approach". The Mathematical Gazette. 95 (533): 327–330. doi:10.1017/S0025557200003193. ISSN 0025-5572. S2CID 123995083.
- ^ Adams, Douglas (1979). The Hitchhiker's Guide to the Galaxy. p. 179-80.
- ^ Adams, Douglas (1980). The Restaurant at the End of the Universe. p. 181-84.
- ^ Adams, Douglas (1985). Perkins, Geoffrey (ed.). The Original Hitchhiker Radio Scripts. London: Pan Books. p. 128. ISBN 0-330-29288-9.
- ^ Diaz, Jesus. "Today Is 101010: The Ultimate Answer to the Ultimate Question". io9. Archived from the original on 26 May 2017. Retrieved 8 May 2017.









![{\displaystyle {\sqrt[{x}]{54}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce344fb05d2962331f08d268334f102b3e5af953)